
TECHNICAL DESCRIPTION OF HYDRODYNAMIC MODELS

THE CHOICE OF DIGITAL MODEL (top of the page)
Several characteristics must be considered in the choice of a digital model. The report by Hay and Co mentions several factors which must be considered. This study recommends two models which could be used for hydrodynamic modeling in estuarine environment (e.g. Fraser): the model of ADCIRC of Dr. Richard A. Luettich Jr. of North Carolina University and Dr. J.J. Westrink of the Notre Dame University as well as model H3D of Dr. James Stronach of Hay and Co.
While basing itself on the criteria defined in this report, the purpose of which was to evaluate the performance of 2D-3D digital models available on the market, the attentive reader will be convinced that our models have even more potential than these two models.
Our 2D and 3D models consist of several standard blocks whose operation is described in Dhatt G and Touzot (1981). Modules more specific to fluid hydrodynamics were developed by Robert J and Mr. Gagnon (1978, 1983, 1994, 2001)
If one uses the finite element method, the quadratic element of T63 type and the traditional temporal resolution method are not appropriate for problems including a too great number of elements: the inversion of the masses and tangent matrices require a great quantity of memory and UCT. We developed (Gagnon, 1994) a quasi-quadratic element of T63 type which requires less memory and UCT without affecting as much quality for the results (Gagnon Mr. and all. 2001). The precision of this element is comparable with that of the traditional quadratic element (Robert, 1978, 1983). However, due to the use of Lax-Wendroft diagram with masses diagonal matrix and temporal 3rd order discretization as well as exact integration of all the equation system's terms, the performance of this hydrodynamic module is much higher than the traditional element. One will find in Gagnon (1994) all the details concerning the hydrodynamic development of the 2D and 3D modules.
The document which follows describes the principal functionalities
of the 2D barotropic and 3D baroclinic models which represent the two extremes
with regard to the degree of sophistication of our models.
2D BAROTROPIC MODULE (top of the page)
The basic equations of the 2D barotropic module are:
Equation of continuity
|
|
Movement's equation according to X and Y
|
|
Diffusion-transport equation
|
|
Considering this formulation, horizontal shearing is expressed
differently according to whether it is
a) The shearing on the surface (wind)
|
|
b) or at the bottom
|
|
In the preceding equations H represent the total depth, ρ the assumed constant density on all the column of water, F the Coriolis forces, τij the horizontal shear stresses in the direction ij, τi( ) the constraint of internal friction at the surface or at the bottom in direction i.
3D BAROCLINIC MODULE (top of the page)
The three-dimensional model's basic equations are based on vertical integration in layers of the continuity, the diffusion-transport and Navier-Stokes equations by considering the constant hydrostatic pressure on a layer. The following equations result from them:
Equation of continuity
|
|
Movement's equation according to X and Y
![]()
|
|
![]()
|
|
Diffusion-transport equation
|
|
with:
|
|
|
|
Considering this formulation, horizontal shearing is expressed differently according to whether it is
a) The shearing on the surface (wind)
|
|
b) At the interface
|
|
c) Or at the bottom
|
|
The density is given by the following equation of state:
|
|
Where the κ and ι coefficients of the equation of state make it possible to adjust the density according to salinity and temperature.
In the preceding equations k indicates an unspecified layer, b the bottom layer, hk the thickness of the layer, Lk the interface k position compared to the free surface,τijthe horizontal shear stresses inside a layer,τiLk the constraint of internal friction at the interface Lk, Sk the salinity of the layer K, Eik the horizontal dispersion coefficients of the layer K in direction i, ρk the mass density of the layer K,ρ0 the reference density.
TECHNICAL CHARACTERISTICS OF OUR MODELS (top of the page)
PHYSICS (top of the page)
Horizontal Turbulence
The horizontal constraints are connected with the law of viscosity of Newton and Stokes. The coefficients used depend on the form of the field and the module speed.
Vertical Turbulence
We use a formulation which is established according to the mixture's length profile and gradient speed. The shearing caused by the wind and the friction is integrated into the formulation. Thus, the parameters used can balance the influence of the Chezy's coefficient for the bottom layer. In the three-dimensional models, the hydrodynamics depends mainly on the friction formulation at the bottom and the constraints at the interface or at the integration boundaries. The numerical behaviour of a case dominated by friction terms allowed Robert (1983) to define a corrected Chezy's coefficient according to the number of layers of the model:
|
|
"This correction compared to the average Chezy's coefficient represents an increase in the shear stress close to the bed". Such a relation allows for a more adequate simulation in the vertical profile speed of a uniform permanent flow. Such a formulation is based on the hypothetical distribution of a mixture's length following the Blumberg's vertical (1978) and is compared advantageously (simpler of use) with the parameterization of the vertical mixture used by Lynch and Werner (1991).
Covering/Uncovering
This algorithm was developed recently. It does not imply a meshing recalculation of the geometrical domain and makes it possible to retain water in the pits at low tide. On the other hand, this algorithm has not been yet validated with real data. It will have also to be added to the 3D baroclinic model.
Baroclinicity
The mathematical formulation of the movement's equations of the 3D module takes into account the density structure. This one is calculated using an equation of state and the diffusion-transport equation (see the equations of this module). It is considered that the hydrodynamic equation's system is uncoupled from the diffusion-transport equation. This assumption is not restrictive at all. It is justified by the fact that inside a time step, the velocity field and the density structure are sufficiently stable enough not to be influenced mutually. One will take into account, at each step of time, any variation in the density structure. It is important to note that the 3D model is a multi-layer model and so it can be used in 2D.
This model proved to be an effective instrument to study and analyze the influence of the density structure on the tidal current propagation in the St. Lawrence estuary. It made it possible to reproduce the principal elements of the estuary's circulation: strong tidal currents in the middling estuary, barotropic and baroclinic instabilities in the maritime estuary. The results obtained with the model demonstrate that the instabilities, caused by the complex estuary's bathymetry and the presence of density gradients, would be at the origin of the two swirls observed in the St. Lawrence maritime estuary.
THE MESHING GENERATION (top of the page)
The meshing generation process is carried out using two softwares: 3D View and Trigrid which can generate a meshing starting from numerical bathymetric data. This is a relatively long and difficult process which requires compromises between the quality of the space resolution and the quantity of calculation points. The density of calculation points is a very restrictive element in the three-dimensional models because computing time increases according to n3.
The last stage of the meshing generation process consists in optimizing the discretization of the geometrical domain. Thanks to an errors estimator, the field is re-meshed in several successive stages in order to prevent the numerical instabilities caused by a wrong discretization of the geometrical domain.
RESOLUTION METHODS (top of the page)
Temporal Solution
In non-permanent mode, one can use several types of numerical diagrams by a very simple choice of parameters. The resolution method chosen by the parameters IMETH (1, 2, 3, 4) and OMEGA (0., .5 and 1.) refers to different incremental substitution methods (Newton-Raphson, Prediction-Correction, Crank-Nicholson, Lax-Wendroft) and to the distribution factor for the resolution diagram (implicit, explicit, semi-implicit)
Horizontal Discretization
Several types of horizontal discretization are used in finite elements: irregular quadrilateral (6 nodes or 9 nodes) and triangles (T3, T3B, T63 and T66). The 2D and 3D modules which are previously described use a T63 type quasi-quadratic irregular triangle. This element is based on the exact integration techniques and the assembly of four subelements defined from linear interpolation functions.
- The U and V components are localised at all the nodes.
- The rise of water level and salinity are calculated only with the top nodes.
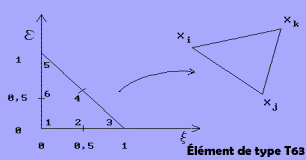
The assembly of the elementary residue with the masses and tangent matrices correspond to the summation on the four subelements, of all the terms considered. Calculations are carried out starting from linear interpolation functions, but the result of the assembly makes it a quasi-quadratic element. The numerical integration of the system equations are then largely simplified, due to the use of a triangle with three nodes. By calculating all the terms, it is possible for us to use all the resolution methods of the time block with this element: Implicit or explicit Euler, Crank Nickolson and Lax-Wendroft.
Vertical discretization
The 3D module uses a multi-layer type vertical discretization. In its current version the layers are of equal depth. We foresee to improve this distribution by proposing variable depth layers.
Potential of development
The potential of development could not be better since we are the developers of these models. In fact, MJL2D and MJL3D contain many modules making it possible to address particular problems which were developed under the direction of Dr. Robert.
The speed of execution of the 2D barotropic module is exceptional, taking into account the mathematical rigour with which the problem is dealt. This module is regarded as a high performance element allowing for consideration of problems comprising a great number of degrees of freedom.
Problems which require a three-dimensional approach are more complex and require an even more rigorous approach. The 3D baroclinic module requires more data-processing resources. The 3D models can be carried out on Pentiums II, III and IV if one has sufficient memory (more than 512 Mega bytes).
Our model will be more user-friendly if a work platform is
entirely dedicated for it. The working station must have precise specifications
with regard to the mother board, the hard disk, the graphics card, video controller
etc... In addition to the finite elements model and the pre-processing and post-processing
modules, a certain number of software must be part of the working station. Being
given the type of authorized licence (exclusive to a site), it is not recommended
to modify the system requirements. Moreover inclusion of other modules or software
could modify the system's performances and give computing times which are not
in conformity with the specifications mentioned in technical documents.
COMPUTING TIME (top of the page)
The speed of execution of the 2D barotropic module is exceptional, taking into account the mathematical rigour with which the problem is dealt. This module is regarded as a high performance element allowing for consideration of problems comprising a great number of degrees of freedom.
Problems which require a three-dimensional approach are more complex and require an even more rigorous approach. The 3D baroclinic module requires more data-processing resources. The 3D models can be carried out on Pentiums II, III and IV if one has sufficient memory (more than 512 Mega bytes).
Our model will be more user-friendly if a work platform is entirely dedicated for it. The working station must have precise specifications with regard to the mother board, the hard disk, the graphics card, video controller etc... In addition to the finite elements model and the pre-processing and post-processing modules, a certain number of software must be part of the working station. Being given the type of authorized licence (exclusive to a site), it is not recommended to modify the system requirements. Moreover inclusion of other modules or software could modify the system's performances and give computing times which are not in conformity with the specifications mentioned in technical documents.
SOFTWARE (top of the page)
COST OF MODELS (top of the page)
2D and 3D hydrodynamic models with finite elements are sold commercially via the company Océanide Inc. The authors of the model are Dr. J.L. Robert of the University Laval and Dr. Mr. Gagnon, Océanide Inc.'s president. The price of 2D-3D model is not fixed yet; its cost will be established according to the various modules included with the basic model and to the accessibility of the required code. Other modules are also available:
APPLICATIONS (top of the page)
When the 2D barotropic module is used in rivers, it is possible to impose the flows on the open limits without forcing the water level or speed.
A special module was developed in order to impose the conditions of water level and currents on the model's open limits. These values are deduced from the harmonic analysis of tidal or current observations. The module uses the algorithm developed by Foreman (1977).
2D BAROTROPIC MODULE (top of the page)
3D BAROCLINIC MODULE (top of the page)
[Home] [Contact Mario Gagnon] [Webmaster]