
DESCRIPTION TECHNIQUE DES MODÈLES HYDRODYNAMIQUES

LE CHOIX DU MODÈLE NUMÉRIQUE (haut de la page)
Plusieurs particularités doivent être considérées dans le choix d'un modèle numérique. Le rapport de Hay and Co. mentionne plusieurs facteurs qui doivent être considérés. Cette étude recommande deux modèles qui pourraient être utilisé pour la modélisation hydrodynamique en milieu estuarien (ex. Fraser): le modèle de ADCIRC du Dr. Richard A. Luettich Jr. de l'université de la Caroline du Nord et du Dr. J.J. Westrink de l'université de Notre-Dame ainsi que le modèle H3D du Dr. James Stronach de Hay and Co.
En se basant sur les critères définis dans ce rapport, qui avait pour but d'évaluer la performance des modèles numériques 2D-3D disponibles sur le marché, le lecteur attentif sera convaincu que nos modèles présentent encore plus de potentiel que ces deux modèles.
Nos modèles 2D et 3D sont constituées de plusieurs blocs standards dont le fonctionnement est décrit dans Dhatt G. et Touzot (1981). Des modules plus spécifiques à l'hydrodynamique des fluides ont été développés par Robert J. et M. Gagnon (1978, 1983, 1994, 2001)
Si on utilise la méthode des éléments finis, l'élément quadratique de type T63 et la méthode de résolution temporelle traditionnelle ne conviennent pas à des problèmes comprenant un trop grand nombre d'éléments: l'inversion des matrices masse et tangente nécessite une grande quantité de mémoire et d'UCT. Nous avons développé (Gagnon, 1994) un élément quasi-quadratique de type T63 qui demande moins de mémoire et d'UCT sans affecter pour autant la qualité des résultats (Gagnon M. et all. 2001). La précision de cet élément est comparable à celle de l'élément quadratique traditionnel (Robert, 1978, 1983). Cependant, grâce à l'utilisation d'un schéma de Lax-Wendroft avec matrice masse diagonale et une discrétisation temporelle du 3 ième ordre ainsi que de l'intégration exacte de tous les termes du système d'équations, la performance de ce module hydrodynamique est de beaucoup supérieure à l'élément traditionnel. On trouvera dans Gagnon (1994) tous les détails concernant le développement des modules hydrodynamique 2D et 3D.
Le document qui suit décrit les principales fonctionnalités des modèles barotrope 2D et barocline 3D qui représentent les deux extrêmes en ce qui concerne le degré de sophistication de nos modèles.
LE MODULE BAROTROPE 2D (haut de la page)
Les équations de base du module barotrope 2D sont:
Équation de continuité
|
|
Équation du mouvement selon X et Y
|
|
Équation de diffusion-transport
|
|
Considérant cette formulation, le cisaillement horizontal s'exprime différemment selon qu'il s'agit
a) du cisaillement en surface (vent)
|
|
b) ou au fond
|
|
Dans les équations précédentes H représente la profondeur totale, ρ la densité assumée constante sur toute la colonne d'eau, f la force de Coriolis, τij les contraintes de cisaillement horizontales dans la direction ij, τi( ) la contrainte de frottement interne en surface ou au fond dans la direction i.
LE MODULE BAROCLINE 3D (haut de la page)
Les équations de base du modèle tridimensionnel sont basées sur l'intégration verticale en couches de l'équation de continuité, des équations de Navier-Stokes et de diffusion-transport en considérant la pression hydrostatique constante sur une couche. Il en résulte les équations suivantes:
Équation de continuité
|
|
Équation de mouvement selon X et Y
![]()
|
|
![]()
|
|
Équation de diffusion-transport
|
|
avec:
|
|
|
|
Considérant cette formulation, le cisaillement horizontal s'exprime différemment selon qu'il s'agit
a) du cisaillement en surface (vent)
|
|
b) aux interfaces
|
|
c) ou au fond
|
|
La densité est donnée par l'équation d'état suivante:
|
|
Où les coefficients κ et ι de l'équation d'état permettent d'ajuster la densité en fonction de la salinité et de la température.
Dans les équations précédentes k désigne une couche quelconque, b la couche de fond, hk l'épaisseur de la couche, Lk la position de l'interface k par rapport à la surface libre, τij les contraintes de cisaillement horizontales à l'intérieur d'une couche, τiLk la contrainte de frottement interne à l'interface Lk, Sk la salinité de la couche k, Eik le coefficients de dispersion horizontal de la couche k dans la direction i, ρk la densité massique de la couche k, ρ0 la densité de référence.
LES PARTICULARITÉS TECHNIQUES DE NOS MODÈLES (haut de la page)
LA PHYSIQUE (haut de la page)
Turbulence horizontale
Les contraintes horizontales s'apparentent à la loi de viscosité de Newton et de Stokes. Les coefficients utilisés dépendent de la forme du domaine et du module de la vitesse.
Turbulence verticale
Nous utilisons une formulation qui est établie en fonction du profil de la longueur de mélange et du gradient de la vitesse. Le cisaillement causé par le vent et celui attribuable au frottement est intégré à la formulation. Ainsi, les paramètres utilisés permettent de pondérer l'influence du coefficient de Chezy dans la couche de fond. Dans les modèles tridimensionnels, l'hydrodynamique dépend principalement de la formulation du frottement sur le fond et des contraintes aux interfaces ou bornes d'intégration. Le comportement numérique d'un cas dominé par les termes de frottement a permis à Robert (1983) de définir un Chézy corrigé en fonction du nombre de couches du modèle:
|
|
"Cette correction par rapport au coefficient de Chézy moyen représente une augmentation de la contrainte de cisaillement près du lit. " Une telle relation permet de simuler plus adéquatement le profil vertical de vitesse d'un écoulement permanent uniforme. Une telle formulation s'appuie sur la distribution hypothétique de la longueur de mélange suivant la verticale de Blumberg (1978) et se compare avantageusement (plus simple d'utilisation) à la paramétrisation du mélange vertical utilisée par Lynch et Werner (1991).
Couvrant/découvrant
Cet algorithme a été développé récemment. Il n'implique pas le remaillage du domaine géométrique et permet de retenir l'eau dans les fosses à marée basse. Par contre, cet algorithme n'a pas encore été validé avec des données réelles. Il devra aussi être ajouté au modèle barocline 3D.
Baroclinicité
La formulation mathématique des équations du mouvement du module 3D tient compte de la structure de densité. Celle-ci est calculée à l'aide d'une équation d'état et de l'équation de diffusion-transport (voir les équations de ce module). On considère que le système d'équations hydrodynamiques est découplé de l'équation de diffusion-transport. Cette hypothèse n'est aucunement restrictive. Elle se justifie par le fait qu'à l'intérieur d'un pas de temps, le champ de vitesse et la structure de densité sont suffisamment stables pour ne pas s'influencer mutuellement. On prendra en considération, à chaque pas de temps, toute variation de la structure de densité. Il est important de noter que le modèle 3D est un modèle multicouche et qu'il peut de ce fait être utilisé en 2D.
Ce modèle s'est avéré un instrument efficace pour étudier et analyser l'influence de la structure de densité sur la propagation des courants de marée dans l'estuaire du Saint-Laurent. Il a permis de reproduire les principaux éléments de la circulation estuarienne: forts courants de marée dans l'estuaire moyen, instabilités barotropes et baroclines dans l'estuaire maritime. Les résultats obtenus avec le modèle ont permis de démontrer que les instabilités, causées par la bathymétrie complexe de l'estuaire et la présence de gradients de densité, seraient à l'origine des deux tourbillons observés dans l'estuaire maritime du Saint-Laurent.
LA GÉNÉRATION DU MAILLAGE (haut de la page)
Le processus de génération de maillage est réalisé à l'aide de deux logiciels : 3D View et Trigrid qui permettent de générer un maillage à partir de données bathymétriques numérisées. C'est un processus relativement long et relativement difficile qui nécessite des compromis entre la qualité de la résolution spatiale et la quantité de points de calculs. La densité de points de calcul est un élément très restrictif dans les modèles tridimensionnels car la quantité de temps de calcul augmente en fonction de n3.
La dernière étape du processus de génération de maillage consiste à optimiser la discrétisation du domaine géométrique. Grâce à un estimateur d'erreurs le domaine est remaillé en plusieurs étapes successives afin de prévenir les instabilités numériques causées par une mauvaise discrétisation du domaine géométrique.
LES MÉTHODES DE RÉSOLUTION (haut de la page)
Solution temporelle
En mode non-permanent, on peut utiliser plusieurs types de schémas numériques par un choix très simple de paramètres. La méthode de résolution choisie par les paramètres IMETH (1, 2, 3, 4) et OMEGA (0., .5 et 1.) font référence à des méthodes de substitution incrémentale différentes (Newton-Raphson, Prédiction-Correction, Crank-Nicholson, Lax-Wendroft) et au facteur de répartition pour le schéma de résolution (implicite, explicite, semi-implicite)
Discrétisation horizontale
Plusieurs type de discrétisation horizontale sont utilisés en éléments finis: quadrilatère (6 noeuds ou 9 noeuds) et triangles irréguliers (T3, T3B, T63 et T66). Les modules 2D et 3D qui sont décrits précédemment utilisent un triangle irrégulier quasi-quadratique de type T63. Cet élément s'appuie sur les techniques de l'intégration exacte et de l'assemblage de quatre sous-éléments définis à partir de fonctions d'interpolation linéaire.
- les composantes U et V sont localisées à tous les noeuds.
- l'élévation du niveau d'eau et la salinité ne sont calculées qu'aux noeuds sommets.
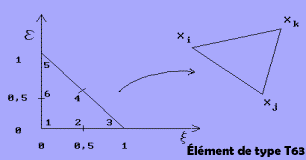
L'assemblage du résidu élémentaire et des matrices masse et tangente correspond à la sommation sur les quatre sous-éléments, de tous les termes considérés. Les calculs s'effectuent à partir de fonctions d'interpolation linéaire, mais le résultat de l'assemblage en fait un élément quasi-quadratique. L'intégration numérique des équations du système est alors grandement simplifiée, dû à l'utilisation d'un triangle à trois noeuds. En calculant tous les termes, il nous est possible d'utiliser toutes les méthodes de résolution du bloc temps avec cet élément: Euler implicite ou explicite, Crank Nickolson et Lax-Wendroff.
Discrétisation verticale
Le module 3D utilise une discrétisation verticale de type multi-couches. Dans sa version actuelle les couches sont d'égale profondeur. Nous prévoyons améliorer cette distribution en proposant des couches de profondeur variable.
Potentiel de développement
Le potentiel de développement ne saurait être meilleur puisque nous sommes les développeurs de ces modèles. En fait, MJL2D et MJL3D contiennent de nombreux modules permettant d'adresser des problèmes particuliers qui ont été développés sous la direction du Dr. Robert.
La vitesse d'exécution du module barotrope 2D est exceptionnelle compte tenu de la rigueur mathématique avec laquelle le problème est traité. Ce module est considéré comme un module à haute performance permettant de considérer des problèmes comportant un grand nombre de degrés de liberté.
Les problèmes qui nécessitent une approche tridimensionnelle sont plus complexes et nécessitent une approche encore plus rigoureuse. Le module barocline 3D nécessite davantage de ressources informatiques. Les modèles 3D peuvent être exécuté sur des Pentiums II, III et IV si on dispose de suffisamment de mémoire ( plus de 512 Méga octets).
Notre modèle aura une plus grande convivialité si une plate-forme de travail lui est entièrement dédiée. Le poste de travail doit posséder des spécifications précises en ce qui concerne la carte mère, le disque dur, la carte graphique, le contrôleur vidéo etc... Outre le modèle aux éléments finis et les modules de pré-traitement et de post-traitement un certain nombre de logiciels doivent faire partie intégrante du poste de travail. Étant donné le type de licence consentie (exclusive à un site), il n'est pas recommandé de modifier la configuration du système. De plus l'inclusion d'autres modules ou logiciels pourraient modifier les performances du système et donner des temps de calculs qui ne sont pas conformes avec les spécifications mentionnées dans les documents techniques.
TEMPS DE CALCUL (haut de la page)
La vitesse d'exécution du module barotrope 2D est exceptionnelle compte tenu de la rigueur mathématique avec laquelle le problème est traité. Ce module est considéré comme un module à haute performance permettant de considérer des problèmes comportant un grand nombre de degrés de liberté.
Les problèmes qui nécessitent une approche tridimensionnelle sont plus complexes et nécessitent une approche encore plus rigoureuse. Le module barocline 3D nécessite davantage de ressources informatiques. Les modèles 3D peuvent être exécutés sur des pentiums II, III et IV si on dispose de suffisamment de mémoire (plus de 512 Méga octects.)
Notre modèle aura une plus grande convivialité si une plate-forme de travail lui est entièrement dédiée. Le poste de travail doit posséder des spécifications précises en ce qui concerne la carte mère, le disque dur, la carte graphique, le contrôleur vidéo etc... Outre le modèle aux éléments finis et les modules de pré-traitement et de post-traitement, un certain nombre de logiciels doivent faire partie intégrante du poste de travail. Étant donné le type de licence consentie (exclusive à un site), il n'est pas recommandé de modifier la configuration du système. De plus l'inclusion d'autres modules ou logiciels pourraient modifier les performances du système et donner des temps de calculs qui ne sont pas conformes avec les spécifications mentionnées dans les documents techniques.
LOGICIELS (haut de la page)
COÛT DES MODÈLES (haut de la page)
Les modèles hydrodynamiques 2D et 3D aux éléments finis sont vendus commercialement par l'intermédiaire de la compagnie Océanide inc. Les auteurs du modèle sont le Dr. J.L. Robert de l'Université Laval et le Dr. M. Gagnon président de Océanide inc. La valeur nominale du modèle 2D-3D n'a pas encore été fixée, son coût sera établi en fonction des différents modules inclus avec le modèle de base et de l'accessibilité du code demandé. D'autres modules sont également disponibles:
APPLICATIONS (haut de la page)
Utilisation en rivière
Lorsque le module barotrope 2D est utilisé en rivière, il est possible d'imposer les débits sur les limites ouvertes sans qu'il soit nécessaire de forcer le niveau d'eau ou les vitesses.
Utilisation en milieu estuarien et côtier
Un module spécial a été développé afin d’imposer les conditions de niveau d'eau et de courants au limites ouvertes du modèle. Ces valeurs sont déduites de l'analyse harmonique des observations de marée ou de courant. Le module utilise l’algorithme développé par Foreman (1977).
MODULE BAROTROPHE 2D (haut de la page)
MODULE BAROCLINE 3D (haut de la page)